Predicting The Great Pumpkin

Thanks to Doc Running who has organized a Halloween blog hop, you are in for a treat from several great math teachers! I've got a big story for you that I hope you'll share with students, and links to more great resources. Read on!

I always smile when I think about the scene in Big where giant Tom Hanks is coincidentally eating a tiny ear of corn. Partly I smile because it’s great comedy—he approaches the task with a seriousness reminiscent of Chaplin eating his shoe.

But I also like this scene because science! Corn (more precisely, maize) was domesticated

around 9000 years ago. Like all domesticated plants, maize has a wild ancestor, in this case a Central American grass called teosinte. The seeds have hard shells and look like rocks when dry to be camouflaged against the ground. They didn’t want to be eaten!

 

University of Wisconsin-Madison

But early farmers selected the most edible and planted them, continuing the process until they created miniature versions of our modern maize. Below are the ancient cobs that archeologists found, measuring just 6 cm ( 2.4 inches). Was Tom Hanks eating a variety of domesticated maize from 4200 BC?

Proceedings on the National Academy of Sciences of the United States of America

Well no, he was actually eating baby corn—modern maize harvested tiny. But still, it’s amaizing how big domesticated corn is compared to its wild ancestor! Impressed? Well then, consider the giant pumpkin. This record holder from 2014 weighed 2323 pounds!

Great Pumpkin Commonwealth

Is this just a normal pumpkin that’s been overfed, or is it some genetic freak? A little of both. The seeds of a monster can sell for thousands of dollars as growers select the genes for giants. But they also tend to these plants with a care usually reserved for royalty—fertilizing, watering, removing pests and turning the pumpkin to avoid cracking or rot over 4 months of growing. And these farmers are doing a great job—nearly every year there has been a new record for heaviest pumpkin ever. 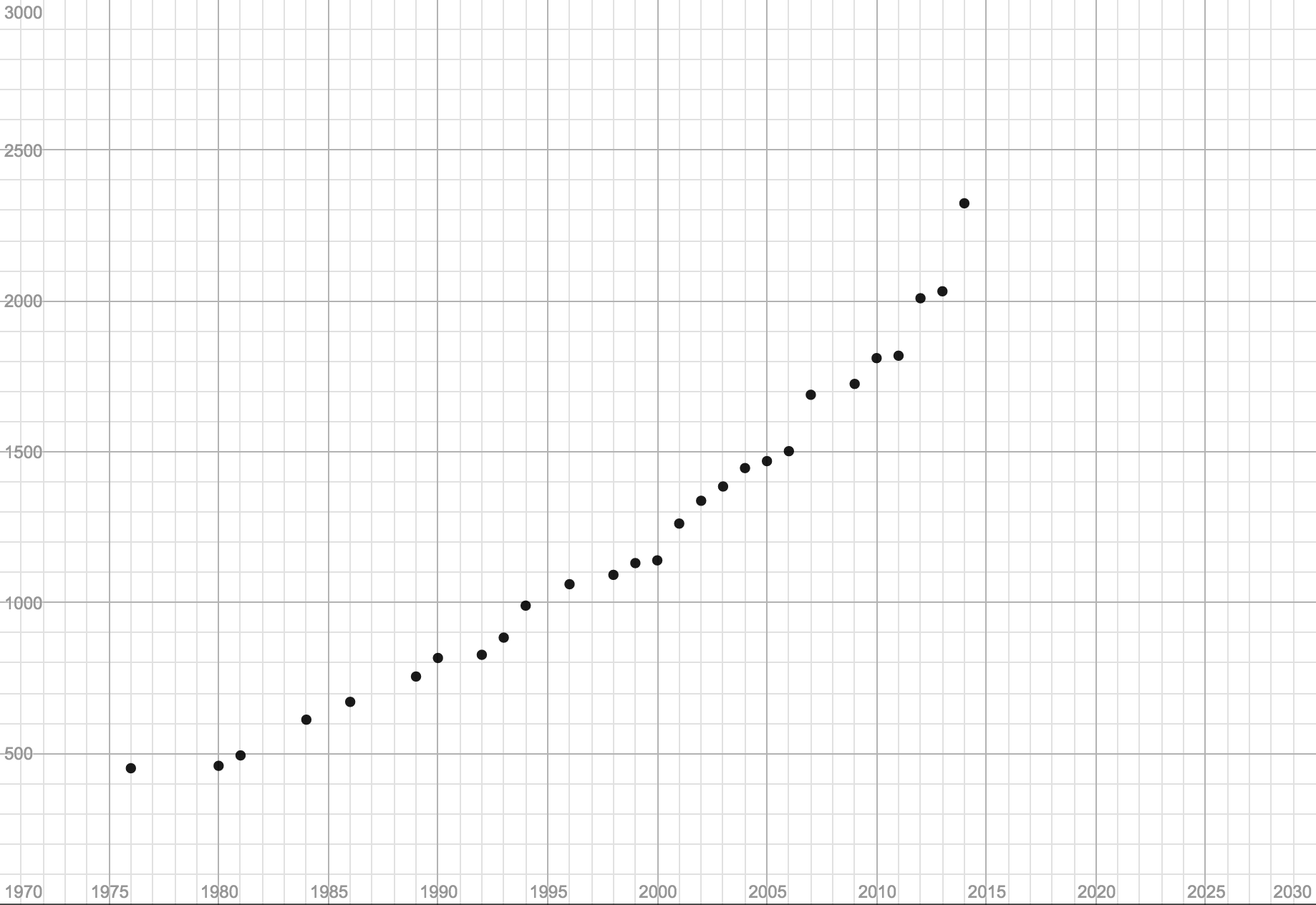In 1976, the record pumpkin weighed only 451 pounds.

In interviews, growers and botanists agree that the records will continue to fall, with some speculating that a 4000 pound pumpkin is close at hand. That’s about the weight of a Ford Taurus! Does the math support this prediction? Let’s look at a graph. The x-axis represents the year and the y-axis represents the weight of the world-record pumpkin for that year.

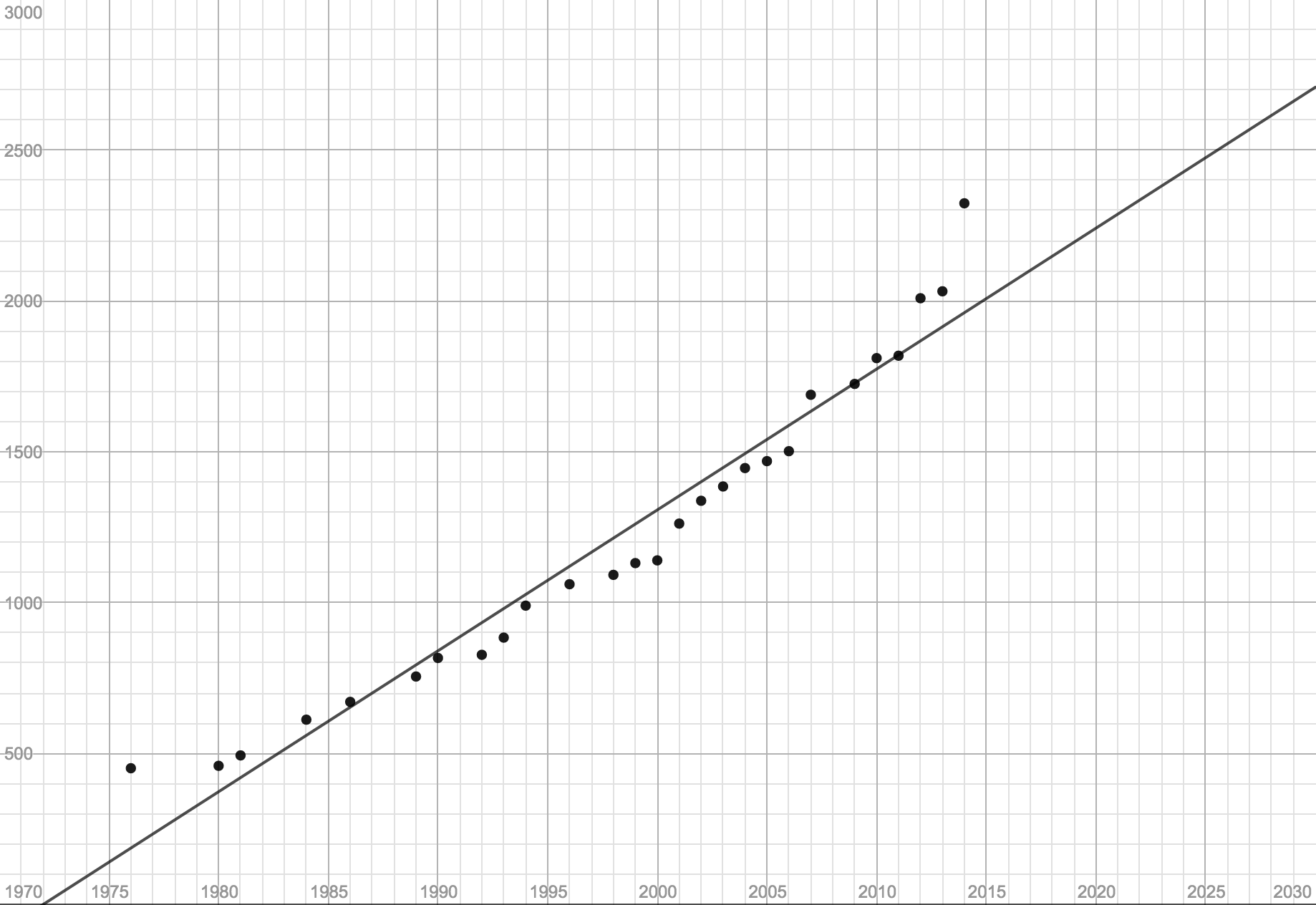
Performing a linear regression is the statistical process of finding the line of best fit for the data:

Wow, fits pretty well, doesn’t it? Hefty slope, right? And yet we can see that starting in 2007, the mass of the pumpkins has often increased at a faster rate than 46.7 pounds per year. Does this mean that a quadratic function would do better? Or how about an exponential function?

Quadratic

Exponential

The quadratic does better than the linear function, and the exponential model seems even better. So let's take the risk and use the exponential to make a prediction. The exponential model predicts the world record in 2015 will be….2252 pounds! Wait, that’s not a world record! The world record is 2323 pounds set last year, and look on the graph—it was pretty far above the exponential curve—a really special pumpkin in the march of the greats. There’s still time for a record breaker, but the biggest pumpkin so far this year is 2230 pounds. I don’t think the record will fall this year, but what do you think?

Either way, pumpkins have come a long way from their humble, wild ancestral origins:

"Cucurbita texana 2" by John D. Byrd, Mississippi State University

Congratulations pumpkin growers. Tom Hanks and maize both grew, but you have truly redefined what it means to grow big!

Now for a couple treats! First off, I made the above graphs using Desmos. I still like and use Geogebra, but I have to praise the uncluttered, intuitive structure of Desmos. Sliders and regressions which take a little work in Geogebra are quick, easy, and they look good right away in Desmos. And of course it's free and you store stuff in your account on their servers. Go try it! Secondly, if you like this post and want to share this adventure with your kids, get the mission for Predicting the Great Pumpkin! Here's another fun one: my Halloween freebie, Candy Jar Estimate. Oh, and check out these other great treats from excellent math teachers!

An InLinkz Link-up